Time Series Clustering using dynamic time warping

Study summarized here

When it comes to unsupervised clustering, Kmeans clustering or Hierarchical clustering are obvious choices. These techniques work well when every data point is iid. When it comes to time series data, and pattern recognition, the temporal value can be utilized to its full potential with time series clustering.

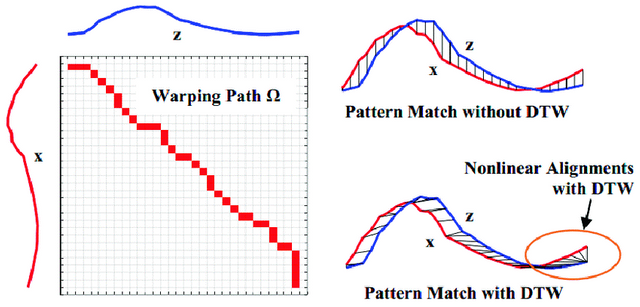
Usually time series clustering algorithms invovle calculating dissimilarity between set of time series and then performing clustering on this dissimilarity scores. One of the powerful dissimilarity measure is dynamic time warping - DTW.

What this post is about

There’s a package in R called dtwclust which is an effective implementation of time series clustering with bunch of different techniques. This article summarizes mathematical formulation of dtw and study of further associated papers.

1. Computing and Visualizing Dynamic Time Warping Alignments in R: The dtw Package
2. Soft-DTW: a Differentiable Loss Function for Time-Series:
3. Fast Global Alignment Kernels
4. Exact indexing of dynamic time warping

The notes are summarized here.

Definition of dynamic time warping distance

The first step in dtw is creating local cost matrix (LCM). Considering two time series as x and y, for each element (i, j) of the LCM, the <math>l^p</math> norm between <math>x_i</math> and <math>y_j</math> must be computed. The nXm distnace matrix of LCMs is computed with further formula,

<math> LCM(i,j) = (∑_v |x_i^v - y_i^v|^p)^1/p </math>

The second step involves finding a path through the nXm matrix of lcm’s that minimizes the alignment iteratively. For the simplest DTW warping path, the constraints include the start point as lcm(1,1) and end point as lcm(n,m) with monotonicity.

So the objective of dtw warping path can be stated as, </br> <math> DTW_p(x,y) = (<span>Σ</span> ^{m_Φ lcm(k)^p} / _{M_Φ})^1/p , ∀ k ∈ Φ </math>

By default, dtw does not consider the l^p norm in above equation, regardless of what is provided in dist.method. For this reason, a special version of DTW2 is registered with proxy by dtwclust (called simply “DTW2”), which also uses dtw for the core calculations, but also uses the l2 norm in the second step.